Research Interests
1. Theory of electronic transport, optical, magnetic properties
of 2D materials and low-dimensional materials.
2. Topological effects on the physical properties in condensed matter systems (Dirac/Weyl semimetals, nodal semimetals, and other topological materials).
2. Topological effects on the physical properties in condensed matter systems (Dirac/Weyl semimetals, nodal semimetals, and other topological materials).
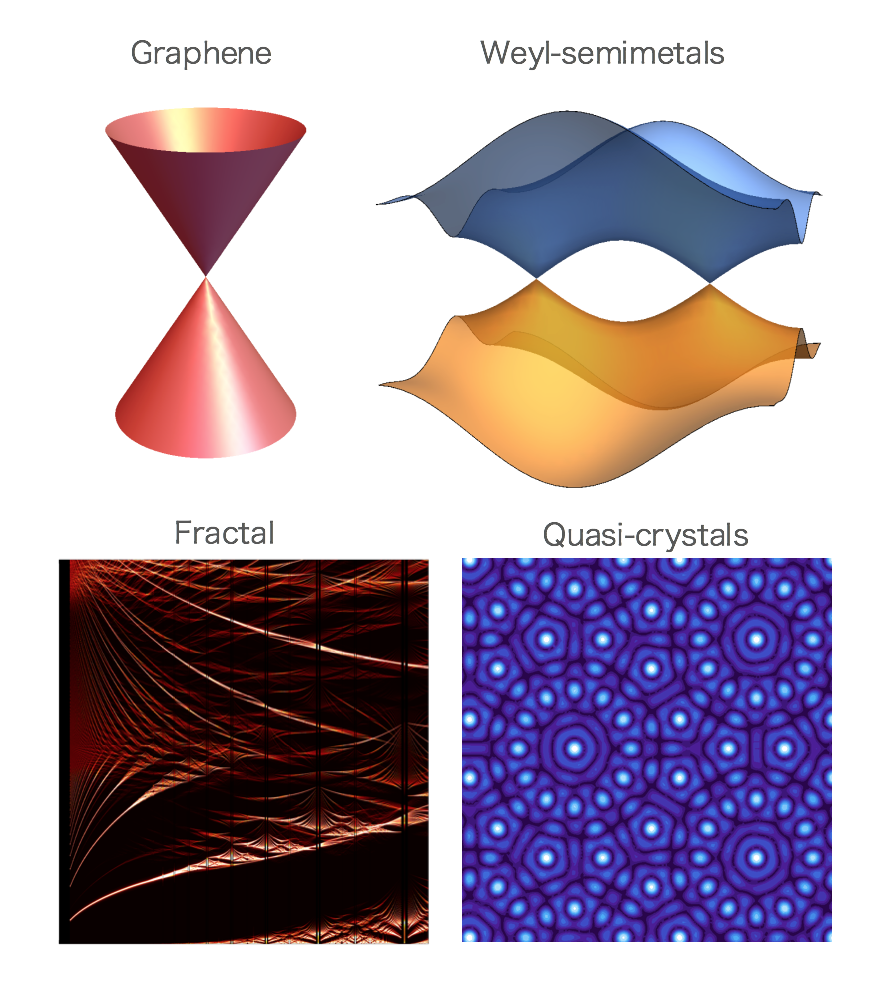
2D materials
Two-dimensional (2D) materials are atomically-thin crystals less than 1 nm thick. For example, graphene, one of the first 2D materials ever created in history, is a single layer of carbon atoms arranged in a honeycomb lattice. Recently the experimentalist successfully fabricated 2D films of various kind of materials, and the physical properties of these system have been one of the most intensively studied topics in condensed matter physics. Interestingly, many of 2D materials often exhibit completely different physical properties compared to the 3D version's. For example, an electron in single-layer graphene behaves like a massless Dirac electron in the relativistic quantum theory, but it never appears in the 3D graphite (or even in bilayer graphene). Likewise, we can make a light-emitting semiconductor by thinning some kind of non-light-emitting 3D semiconductor down to monolayer. It is also possible to make a hybrid material just by stacking different 2D materials, and realize a bizarre nature never found in the original materials.
Two-dimensional (2D) materials are atomically-thin crystals less than 1 nm thick. For example, graphene, one of the first 2D materials ever created in history, is a single layer of carbon atoms arranged in a honeycomb lattice. Recently the experimentalist successfully fabricated 2D films of various kind of materials, and the physical properties of these system have been one of the most intensively studied topics in condensed matter physics. Interestingly, many of 2D materials often exhibit completely different physical properties compared to the 3D version's. For example, an electron in single-layer graphene behaves like a massless Dirac electron in the relativistic quantum theory, but it never appears in the 3D graphite (or even in bilayer graphene). Likewise, we can make a light-emitting semiconductor by thinning some kind of non-light-emitting 3D semiconductor down to monolayer. It is also possible to make a hybrid material just by stacking different 2D materials, and realize a bizarre nature never found in the original materials.
Topological materials
Topology is an absolute mathematical idea that describes geometrical properties, but it is also useful to characterize the inherent nature of condensed matter. Recently, physicists found a number of material classes having the non-trivial topology in the quantum state, which is characterized by a mathematical analog such as Moebius's ring and vortex etc. Non-trivial topology always gives rise to non-trivial physical properties, such as the energy band touching (e.g., graphene) and/or the special surface states. We are theoretically searching for the exotic nature of these novel materials by calculating various kind of physical observables.
Topology is an absolute mathematical idea that describes geometrical properties, but it is also useful to characterize the inherent nature of condensed matter. Recently, physicists found a number of material classes having the non-trivial topology in the quantum state, which is characterized by a mathematical analog such as Moebius's ring and vortex etc. Non-trivial topology always gives rise to non-trivial physical properties, such as the energy band touching (e.g., graphene) and/or the special surface states. We are theoretically searching for the exotic nature of these novel materials by calculating various kind of physical observables.